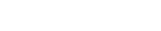Jednoręki bandyta to kolokwialna nazwa automatu, który można spotkać w kasynach na całym świecie. Zasady gry są proste: wrzucamy monety, pociągamy za rączkę i czekamy, aż automat się zatrzyma. Jeśli mamy szczęście, wygrywamy więcej, niż wrzuciliśmy. Teraz załóżmy, że mamy do wyboru K automatów – który z nich powinniśmy wybrać? Ten wpis przedstawia propozycję taktyki, która zwiększa nasze szanse wygranej dzięki koncepcjom statystycznym.
Założenia
Żeby utożsamić czytelnika z problemem, wprowadźmy pewien scenariusz.
Mamy paskudny nawyk uprawiania hazardu. Uzależnienie opuści nas dopiero po rozegraniu 1000 gier. Będziemy grać na trzech dostępnych maszynach. Każda maszyna ma stałe, nieznane nam prawdopodobieństwo wygranej (wartość od 0 do 1). Wszystkie pieniądze, które mamy, dostaliśmy od kochanej babci pod choinkę, więc przegrana nawet złotówki jest dla nas bardzo bolesna.
Rozwiązanie zdroworozsądkowe
Co podpowiada nam intuicja? Pewna liczba monet wrzucona do maszyny pozwoli nam oszacować, jak często konkretny jednoręki wygrywa. Po zagospodarowaniu pewnej ilości N dla każdej maszyny otrzymamy wartości:
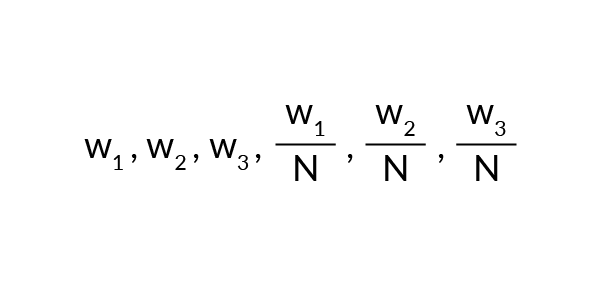
Rysunek 1. obrazuje wyniki symulacji gier dla różnych wartości N. Odbywając X = 100 sesji po 1000 gier, możemy estymować wartość oczekiwaną zwrotu. Przed każdą z sesji zostały wygenerowane losowe wartości prawdopodobieństwa wygranej każdej z maszyn (z przedziału 0 – 0,5). Obserwujemy duży szum między estymacjami, czego przyczyna tkwi w małej liczbie X symulowanych sesji. Im byłaby ona większa, tym wartość średnia próby bliższa byłaby prawdziwej wartości oczekiwanej. Korzystając z regresji, zakładamy wpływ szumu na uzyskane wartości. Rysunek 1. zawiera dodatkowo wykreślenie modelu (regresja jądrowa z bazową funkcją radialną) dopasowanego do danych. Wskazuje nam przewidywaną wartość zwrotu w zależności od N monet zainwestowanych w każdą z maszyn.
 Rysunek 1. Regresja na symulacjach gry intuicyjnej sugeruje, że najlepiej umieścić po 25 monet w każdej z maszyn, a następnie zagrać va banque
Rysunek 1. Regresja na symulacjach gry intuicyjnej sugeruje, że najlepiej umieścić po 25 monet w każdej z maszyn, a następnie zagrać va banque
Podejście Bayesowskie
Innym podejściem będzie próba szacowania rozkładów prawdopodobieństwa nad wartościami parametrów. Twierdzenie Bayesa pozwala nam sprecyzować procedurę modyfikacji naszych oczekiwań dotyczących wartości, które mogą przyjmować prawdopodobieństwa wygranej konkretnej maszyny.
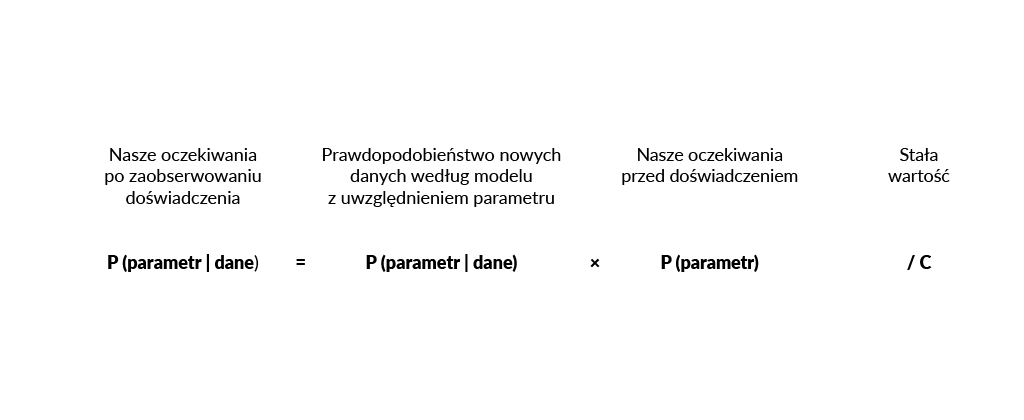 Od naszego wyboru rozkładu statystycznego P (parametr) wiele zależy. Dobry wybór pozwala bowiem na duże ułatwienia w rozumowaniu, a więc wnioskowaniu i predykcji. W naszym problemie modelowania wybieramy jeden z rozkładów należących do rodziny Beta. Argumentujemy to cechą: przemnożony przez funkcję prawdopodobieństwa danych P (dane | parametr) skutkuje znowu rozkładem z tej samej rodziny. Dzięki temu wyniki estymacji z poprzedniej iteracji (po wrzuceniu monety po raz n-ty) możemy umieścić jako nasze założenia startowe P (parametr) do wnioskowania o P (parametr | dane) dla kolejnej gry.
Od naszego wyboru rozkładu statystycznego P (parametr) wiele zależy. Dobry wybór pozwala bowiem na duże ułatwienia w rozumowaniu, a więc wnioskowaniu i predykcji. W naszym problemie modelowania wybieramy jeden z rozkładów należących do rodziny Beta. Argumentujemy to cechą: przemnożony przez funkcję prawdopodobieństwa danych P (dane | parametr) skutkuje znowu rozkładem z tej samej rodziny. Dzięki temu wyniki estymacji z poprzedniej iteracji (po wrzuceniu monety po raz n-ty) możemy umieścić jako nasze założenia startowe P (parametr) do wnioskowania o P (parametr | dane) dla kolejnej gry.Rozkład danych (ponieważ możemy tylko wygrać lub przegrać w pojedynczej grze) ma postać:
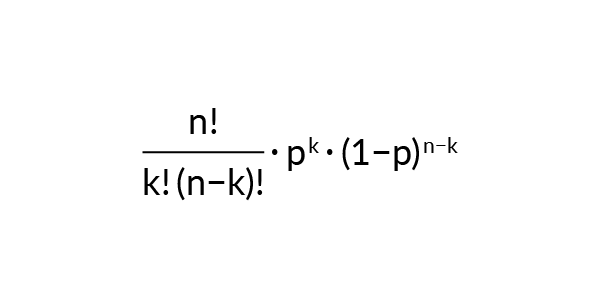
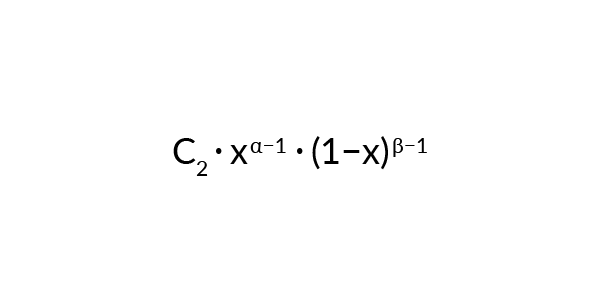
Wymnożenie obydwu funkcji i normalizacja sprawia, że nowe P (parametr) będzie miało postać następującej funkcji:
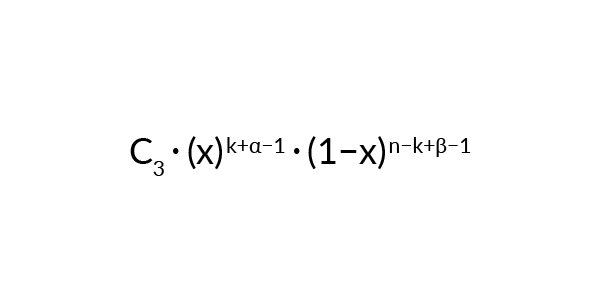
Symulacja szacowania rozkładu, z którego w statystycznym rozumieniu w konkretnej maszynie „było generowane” prawdopodobieństwo wygranej, przedstawiona jest na rysunku poniżej (Rysunek 2.). Zauważmy, że założeniem w tej sytuacji (rysunek 1 z 10) była całkowita niewiedza o naturze maszyny – każda wartość parametru jest w naszym przypadku równie prawdopodobna. Rozkład Beta przybiera postać rozkładu jednostajnego dla swoich parametrów równych 1.
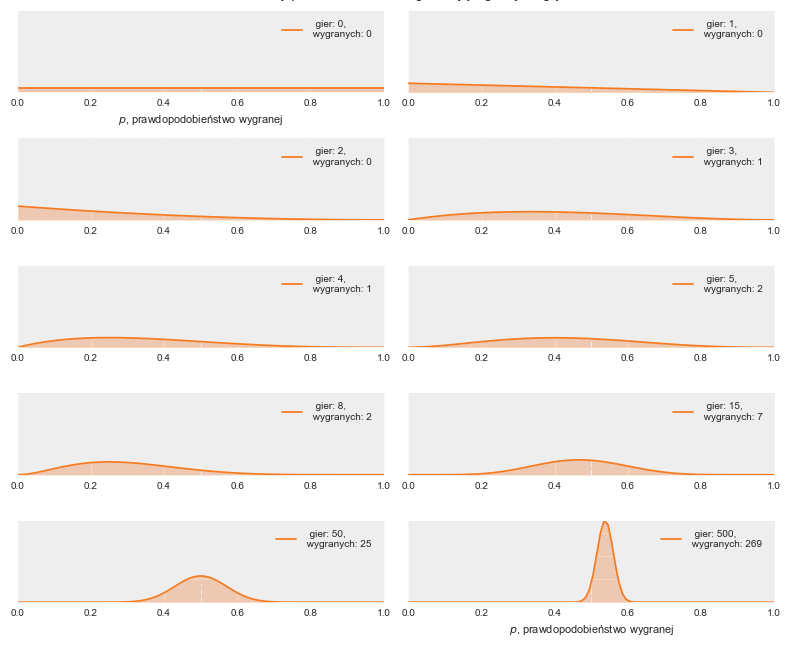 Rysunek 2. Proces iteracyjnego szacowania rozkładu, z którego pochodzi prawdopodobieństwo wygrania automatu
Rysunek 2. Proces iteracyjnego szacowania rozkładu, z którego pochodzi prawdopodobieństwo wygrania automatu
Próbkowanie Thompsona
Powyżej ustaliliśmy, że umiemy modelować naszą niepewność w odniesieniu do parametru konkretnej maszyny. Ostatnim koniecznym krokiem w procedurze gry jest wybór, do której maszyny w danym momencie wrzucić monetę, gdy mamy ogląd parametrów modelu. Aby zminimalizować liczbę monet wrzucanych heurystycznie, korzystamy z metody zwanej próbkowaniem Thompsona. Każdy rozkład przypisany konkurującym o nasze pieniądze maszynom jest jednorazowo „próbkowany”, a moneta zostaje wrzucona do maszyny, z której próbka symulowanego rozkładu była większa niż pozostałe. Ta taktyka pozwala nam pokonać ograniczenie poprzedniej – nie stawiamy całej puli va banque na najbardziej obiecującego kandydata. Inwestujemy natomiast proporcjonalnie do szans, że dany parametr jest większy od pozostałych.
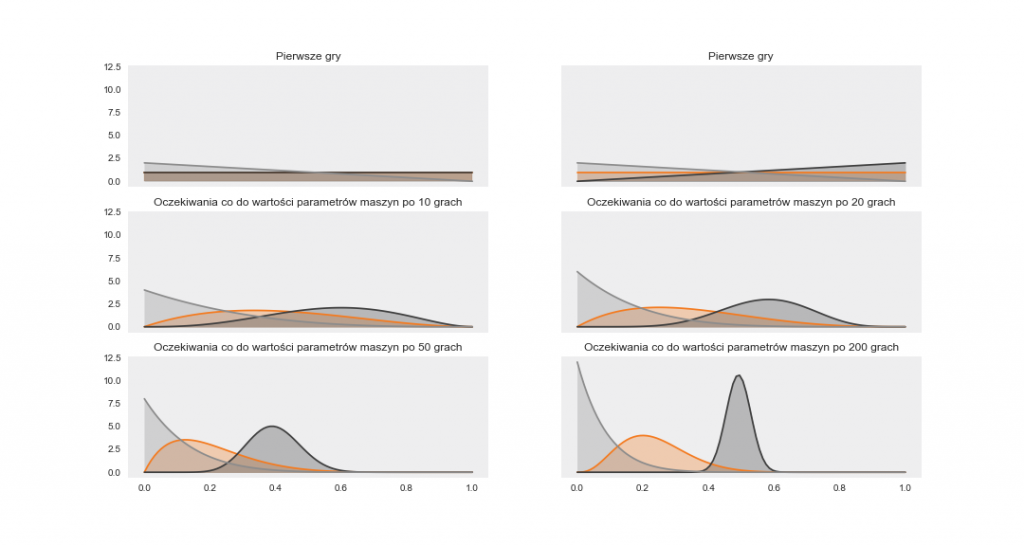 Rysunek 3. Estymacja każdego z rozkładów parametrów trzech maszyn warunkowana wynikami próbkowania Thompsona
Rysunek 3. Estymacja każdego z rozkładów parametrów trzech maszyn warunkowana wynikami próbkowania ThompsonaPowtarzając powyższe doświadczenie dla różnych ukrytych parametrów maszyn, otrzymujemy wartość oczekiwaną wygranych gier. Wykreślamy tę wartość na tle intuicyjnej taktyki (odniesienie do Rysunku 4.)
Podsumowanie
Na Rysunku 4. możemy zobaczyć, że na tym etapie estymowana wartość oczekiwana zwrotu z taktyki nr 2 jest większa od jej estymacji dla taktyki nr 1 i w tym momencie zatrzymujemy rozumowanie, pozostawiając pewne ważne kwestie statystyczne do wyszukania w literaturze.
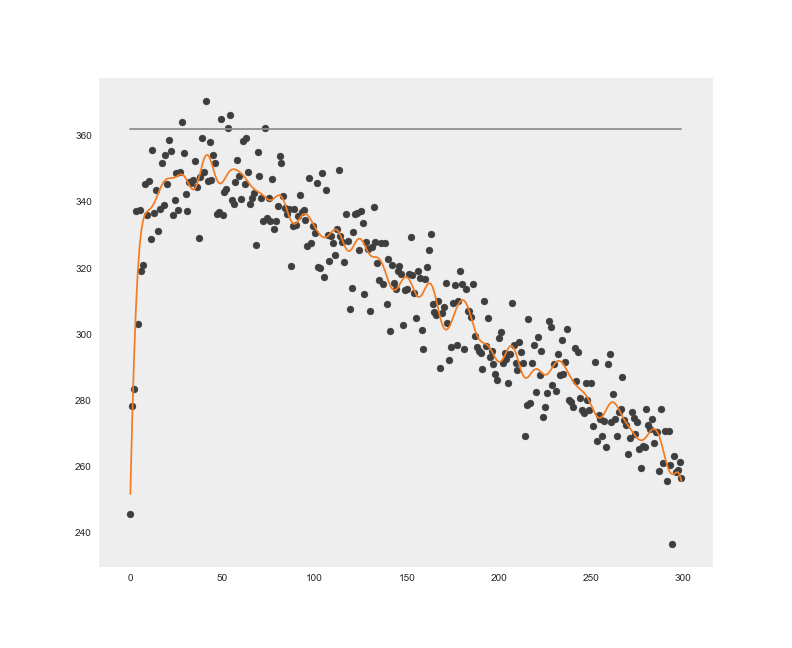 Rysunek 4. Porównanie wyników symulacji wielu gier w celu wyboru lepszej taktyki
Rysunek 4. Porównanie wyników symulacji wielu gier w celu wyboru lepszej taktykiW artykule przedstawiłem wstęp do zagadnienia nazywanego multi-armed bandid. Bayesowska teoria decyzji pozwala nam wyprowadzić dla tego problemu optymalną taktykę znajdywania kompromisu eksploracyjno-eksploatacyjnego. Algorytmami z tej rodziny estymujemy nie tylko cechy automatów (co jest dosyć niszowym zajęciem), ale przede wszystkim modelujemy cechy zarówno produktów (tj. reklamy, artykuły, wersje ofert lub wizualizacji strony), jak i samego użytkownika (np. demografia). Wiedza o tych cechach i odpowiednie dostosowywanie się jest kluczowe dla firm maksymalizujących swoje przychody w sieci.
Mateusz Łukasik – Data Scientist w Onwelo. Zawodowo tworzy systemy ekstrakcji i wnioskowania z danych. Prywatnie fan statystyki bayesowskiej oraz zarówno „dense”, jak i deep learningu.
Zostaw komentarz
Polecamy
Sztuczna inteligencja w wykrywaniu zagrożeń bezpieczeństwa IT
Cyberbezpieczeństwo to nie tylko zaawansowane technicznie systemy zabezpieczeń w dużych firmach czy wojsku. To także nasze prywatne bezpieczeństwo, walka z zagrożeniami i ich prewencja w codziennym życiu oraz wiedza o bezpiecznym korzystaniu z internetu. Adam Kowalski-Potok, nasz Seurity Engineer, opowiada jak AI i jej rozwój wpływa na wykrywanie zagrożeń w cyber security.
Budowanie systemów biznesowych z zastosowaniem generatywnej sztucznej inteligencji
Generatywne AI ma potencjał do automatyzacji zadań zajmujących dziś do 70% czasu pracowników. Dlaczego platforma OpenAI nie wystarczy do wykorzystania pełni tych możliwości? Przed nami artykuł Łukasza Cesarskiego i Marka Karwowskiego z Onwelo powstały na bazie prezentacji wygłoszonej podczas konferencji „Transformacje cyfrowe dla biznesu”.
Data & Analytics – architektura systemów jutra
Jaka jest historia inżynierii danych? Jak przebiegał rozwój technologii i na jakie trendy zwraca obecnie uwagę świat? Marek Kozioł, Data Solution Architect i Arkadiusz Zdanowski, Cloud Data Engineer & Team Leader w Onwelo opowiedzieli o tych zagadnieniach podczas konferencji „Transformacje cyfrowe dla biznesu”. Zapraszamy do lektury artykułu przygotowanego na bazie tego wystąpienia.
Sztuczna inteligencja w wykrywaniu zagrożeń bezpieczeństwa IT
Cyberbezpieczeństwo to nie tylko zaawansowane technicznie systemy zabezpieczeń w dużych firmach czy wojsku. To także nasze prywatne bezpieczeństwo, walka z zagrożeniami i ich prewencja w codziennym życiu oraz wiedza o bezpiecznym korzystaniu z internetu. Adam Kowalski-Potok, nasz Seurity Engineer, opowiada jak AI i jej rozwój wpływa na wykrywanie zagrożeń w cyber security.
Budowanie systemów biznesowych z zastosowaniem generatywnej sztucznej inteligencji
Generatywne AI ma potencjał do automatyzacji zadań zajmujących dziś do 70% czasu pracowników. Dlaczego platforma OpenAI nie wystarczy do wykorzystania pełni tych możliwości? Przed nami artykuł Łukasza Cesarskiego i Marka Karwowskiego z Onwelo powstały na bazie prezentacji wygłoszonej podczas konferencji „Transformacje cyfrowe dla biznesu”.